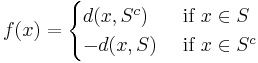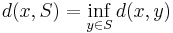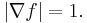Signed distance function

In mathematics and applications, the signed distance function of a set S in a metric space determines how close a given point x is to the boundary of S, with that function having positive values at points x inside S, it decreases in value as x approaches the boundary of S where the signed distance function is zero, and it takes negative values outside of S.

Formally, if (X, d) is a metric space, the signed distance function f is defined by

f(x)= \begin{cases} d(x, S^c) & \mbox{ if } x\in S \\ -d(x, S)& \mbox{ if } x\in S^c \end{cases}

where

d(x, S)=\inf_{y\in S}d(x, y)

and 'inf' denotes the infimum.

If S is a subset of the Euclidean space Rn with piecewise smooth boundary, the signed distance function is differentiable almost everywhere, and its gradient satisfies the eikonal equation

|\nabla f|=1.

Algorithms for calculating the signed distance function include the efficient fast marching method and the more general but slower level set method.

Signed distance functions are applied for example in computer vision.

See also

References